The CAGED Guitar System Explained
The CAGED guitar system can be very useful to help you find your way around the fretboard. The idea is based on the relationship between common major chord and major scale shapes. It is also a very useful method for visualising chord tones across the neck of the guitar. If you can easily find the notes on the fifth and sixth strings of the guitar then all it takes is a bit of practice with the CAGED system and you will be able to find any major chord tone very easily anywhere on the neck. There are two main things you need to learn. The first is the order of the chords always remains in the same sequence C A G E D starting from the C or if you were starting from the G then the order would be G E D C A because after the D chord it starts over again from the C. This makes more sense when you can see it in diagram form as shown below.
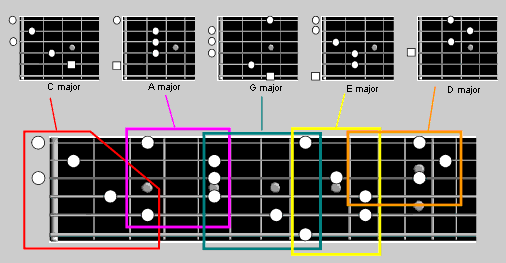
Study the picture above and note how the five chord patterns overlap with each other. Once you get used to visualising the CAGED chords across the neck like this you will find chord tones very easy. Don’t forget the order stays the same, G will always overlap with E etc. The next picture shows the same CAGED sequence starting from a different place to give you the idea.
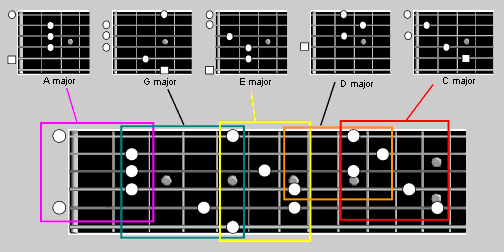
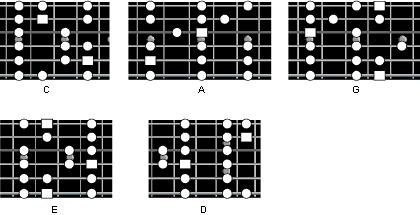
The CAGED system also helps us with playing the major scales. As you have seen in the example above it’s quite easy to get used to the finding the chord tones anywhere on the neck as long as you can quickly find the root notes on the guitar strings. When you learn the major scale positions for the guitar it is a lot to have to remember. This gets even harder when you have to think about these positions in twelve different keys. By combining the major scales with the CAGED sequence of chords this task becomes much easier. By getting used to the relationship between the chords and the scales you will start to realise that remembering these scale positions and being able to find them in any key becomes a lot easier. Study the diagrams below and practice playing with these chord shapes and scales across the fretboard. It might seem a lot of work at first but you will get used to it quite quickly. The CAGED guitar system is a great method to help you find your way around the neck so keep at it and in a few months you should playing the guitar without thinking.
Recent Comments